Web site logical path: [www.psy.gla.ac.uk] [~steve] [best] [this page]

Effect size

Preface

There is an emerging argument that effect size does not solve all those deficiencies: see the last section "Beyond effect sizes".

Main part of this page

Whereas statistical tests such as a t-test aim to tell you what degree of certainty to attribute to the possibility that a difference is not an accident but an effect, another important question is "How important is that difference (if real)?". I shall use the term "effect size" as a general title for this whole question; group all statistical tests of effect size into one topic within the general question; and the issue of which of the alternative stats tests (e.g. "Cohen's d") is best as a subtopic.

Bloom84 gives a powerful argument about how to use effect sizes in planning a programme of applied research.

The main point of measuring effect sizes is to compare the relative importance of different effects, phenomena. An example from psychology illustrates this, by comparing established gender effects -- and how some are really big, but many others of small, even negligible, practical importance.

Comparing effect sizes: getting a sense of the range

These would be even better by using sections below to bring out predictions, given a specific effect size e.g. the CLES which tells you what are the chances, if you pick one random male and one random female, of them differing on a given effect in the predicted direction. I.e. It would be good to add a 3rd col. that shows the odds, given 1M and 1F randomly taken, having a difference in the trait in the same direction as the diff. in the means for that trait.

New Sci, Gender effects table

Explanation of the table below: Diff. between males and females (effect size in StdDev units). Colour of the number shows which sex does better. There are 6 more items in (the bottom of) the original table.

TRAIT	Effect size	Odds of one random pair showing the effect
Gender identity	11.0 - 13.2	-
Sexual orientation	6.0 - 7.0	-
Preference for boy's toys	2.1	0.92
Height	2	0.92
Preference for girl's toys	1.8	0.9
Physical aggression	0.4 - 1.3	0.72
Empathy	0.3 - 1.3	0.71
Fine motor skills	0.5 - 0.6	0.65
Mental rotation	0.3 - 0.9	0.66
Assertiveness	0.2 - 0.8	0.64

Alternative stats measures of effect size

Cohen94 suggests using confidence intervals.

Rough ideas on what size effects are small / medium / large

	Micro	Small	Medium	Large	Huge or Very big	Gigantic
Cases: → Measures ↓	Time of day effects on school tests [9]	Difference between the heights of 15 and 16 year old girls in the USA.[1]	M vs. F verbal fluency[2]	Difference between the heights of 13 and 18 year old girls in the USA.[3]	Female vs. Male height[4] Learning in school class vs. 1:1 tutoring[5]	Biological sex affects gender identity[6]
Cohen's d	e.g. ≤ 0.03	0.2 - 0.3	≈ 0.5	0.8 - or larger	2	12
[7] r (correlation coeff.) [11]	-	0.1 - 0.3 ≈ 0.1	0.3 - 0.5 ≈ 0.3	0.5 ≈ 0.5	-	-
R2: % of variance explained	-	1%	9%	25%	-	-
R2: (≈ ≈ Partial eta-squared)	-	0.02	0.13	0.26	-	-
Generalized eta-squared {η_G^2} [8]	-	0.02	0.13	0.26	-	-
Partial eta-squared (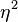)	-	0.01	0.06	0.14	-	-
Odds ratio	-	-	-	-	-	-
Confidence interval	-	-	-	-	-	-

Lit. refs for the table above

1. Mike Clark's slides on effect sizes:   PDF on his web site   (PDF local copy).
2. New Scientist table of gender-sex effects table Spinney, Laura (2011) "Boy brain, girl brain: How the sexes act differently" New Scientist, no.2802, 8 March 2011 http://www.newscientist.com/article/mg20928021.400-boy-brain-girl-brain-how-the-sexes-act-differently.html
3. See [1]
4. See [2]
5. Bloom84 mentions it.
6. See [2]
7. Cohen, J. (1988) Statistical power analysis for the behavioral sciences (2nd ed.) (Hillsdale, NJ: Erlbaum)
   Also: Field,Andy (2013) Discovering Statistics using IBM SPSS 4th edition p.267
8. Cohen, J. (1988) cited above: p.286ff. for some of the effect sizes e.g. for eta-squared.
9. Bakeman, R. (2005) "Recommended effect size statistics for repeated measures designs" Behavior Research Methods vol.37 no.3 pp.379-384 doi:10.3758/BF03192707; criticising Cohen (1988) (see [7]) pp.413-414.
10. Sievertsen et al. 2016
11. Cohen,J. (1992) "A power primer" Psychological Bulletin Vol.112. No.1 pp.155-159 doi:10.1037/0033-2909.112.1.155 In this paper, Cohen expresses small, medium and large effect sizes, not as a range of values, but in terms of a central value for each category.

Other notable cases include:

• Very big.   Particle physicists require a (Cohen's d) effect size of 5 (between "Very Big" and "Gigantic") before declaring the discovery to have been established of a new particle (e.g. the Higgs boson) (wikipedia entry).
• Very small.   This paper about the effect on school tests of the time of day when the child takes it, Sievertsen et al. 2016, has a huge dataset, impeccable stats, and goes the extra mile by providing information to help judge the data against relevant contextual standards. But the effect sizes are still minute: a new category of "micro". It reports a variety of (Cohen's d) effect sizes in the range 0.03 - 0.005.

Different meanings for "Important", and so for "effect size"

But there are different senses of "important" for effects.

Some different senses of "how important" (A plan for future subsections)

1. First: senses of the basic 'how important is this effect'?
2. Contextual issues: what comparisons in each given context are relevant in interpreting whether a given shift (in the mean) is important.
   1. Comparing to what other effects / causes? Even if the experiment did not directly compare to some reference condition, this may be what most readers would find meaningful e.g. comparing a drug to "treatment as usual"; comparing an anti-depressant to regular exercise (now surely the most relevant comparison).
   2. Comparing in what units? e.g. in education, giving an effect size in statistical units may not be as meaningful as in an external unit such as grades e.g. "the intervention increased learners' grades on average by 0.5 (or by 2) grades".
   3. Comparing in what units? e.g. in education, giving an effect size in statistical units may not be as natural as reporting in an intrinsic unit e.g. the intervention resulted in the absolute amount learned (normalised gain) in the experimental group was 2 (or in fact 3) times that learned in the control group (Crouch & Mazur 1993?).
3. What proportion of the sample (or population) did the effect apply to?
4. Somewhere have a section on really big and really small specifically educational effects (including chick-sexing).
5. Cost-effectiveness. In almost any practical context it isn't just an issue of how much good you do, but also of how cheaply it can be done — because with a given amount of resource, you can do more good to more people by a cheap effect than by an expensive one.
6. Unexpectedness w.r.t. theory

What proportion of the sample (or population) did the effect apply to? [C]   #idiff

In these cases, it is of great interest to report what the proportion is of the sample to which it applies. You may or may not agree with Rousselet's labelling of this as a type of "effect size", but perhaps you should in any case consider doing this routinely. Reporting the percentage is useful; a sign test gives the probability of this being by chance.

Note that in this case, really the tacit hypothesis is that the distribution is not normal, but bimodal: a population for which the effect "works", and another for which it doesn't.

Basic approach: StdDev units

From the wikiP page on the Normal distribution; Section on standard deviation and tolerance intervals As mentioned above, elementary particle physicists use the convention of only declaring a discovery when the effect size is 5 (or more): 99.99994% of the data is within 5 SDevs of the mean (or the chance of observing such a data set by chance is about 1 in 1,700,000 or nearly one in two million).

• Given a specific ES, show what % of the old data would be passed.
  The table above is 2-tailed. But with a proven effect with an effect size of 2 (for example) we probably want to know how much of the original data is above 2 stdDevs (one-tailed). To calculate this:
  • Go to this online calculator;
  • (Leave the mean set to 0, the SDev to 1, and the radio button "Above" selected;)
  • Fill in "2" in the box beside "Above", and click "Recalculate".
  It will show the "Area" as 0.0228, which means 2.28% of the data is more than 2 SDevs greater than the mean.
  So if you applied an intervention with an effect size of +2, then without it only 2.28% of a sample score that highly or better, but with it 50% will score that highly.
• If I took one Participant from the midpoint (mean = median) of the old distribution, applied the intervention to her/him alone, then where would we expect them to move to relative to the old distribution? == They were at percentile 50, they would move to which percentile? [E.g. ES = 2, then percentile 50 --> 98; rank 50 --> 2nd] [E.g. ES = 1, then percentile 50 --> 84; rank 50 --> 16]
• [weather extreme events] Given a (small) shift in the mean, what does this do for frequency of datum-s up at the extreme of a distribution? E.g. 100 year storms.
• Odds, in gender effects, of randomly picking 1 M, then 1 F and having the difference on the measure be in the expected direction. Or not. Equally for any effect, pick one value from control group and one from expt group: what chance of these two data being in the expected order.

Then say:
How much in percentiles does a given ES mean?
Or for A vs. B: for a given ES, what are the odds of a random A and B that
they show the right direction for the overall effect?

CLES: chances of a random pair showing the effect

How much of the variance is explained

Other sections / issues about effect size

Cases with small stats effect size, yet importance of other kinds

Sievertsen

Carrying plants out of hospital wards at night, back again during the day.

Unexpectedness w.r.t. theory [F]

I.e. if you want to do immediate practical good to learners, then low ES means it isn't a good investment. However from the viewpoint of theoretical rather than applied research, then the more unexpected an effect, the more valuable it is regardless of effect size. Put another way: a datum which is highly expected has little information value, but one which is highly unexpected (if it can be trusted) has very high information content. Put still another way: for theory-directed research especially, the importance of an effect does not only depend on the size of the difference between an actual observation and a theory-predicted observation but also on the confidence in the surprising measure and the confidence in the prediction.

This is also a way to begin to think about how to reason about the relative value of different bits of qualitative research.

Cost effectiveness [E]

Aveyard et al. (2016) "Screening and brief intervention for obesity in primary care: a parallel, two-arm, randomised trial" The Lancet doi:10.1016/S0140-6736(16)31893-1

Wright Brothers

"They made the first controlled, sustained flight of a powered, heavier-than-air aircraft on December 17, 1903, four miles south of Kitty Hawk, North Carolina, USA." "The brothers' fundamental breakthrough was their invention of three-axis control, which enabled the pilot to steer the aircraft effectively and to maintain its equilibrium. This method became and remains standard on fixed-wing aircraft of all kinds."

By 1909? the modern aircraft had arrived. By 1910 it had been used usefully by the military (both reconnaissance, and dropping bombs).

Robert Stephenson's "Rocket" steam railway locomotive (1829):

• Single pair of driving wheels.
• * Multiple fire tube boiler
• * Blast pipe: using exhaust steam to force a draft through the fire and boiler.
• Less vertical, more nearly horizontal cylinders: better ride of the loco on the track.
• * Pistons directly connected to driving wheels (no gearing used).
• Firebox separate from boiler. I.e. water jacket round firebox was primary heating place; firetubes in boiler did additional heating.

Hake survey

Meta-analysis