Last changed
27 Dec 2022 ............... Length about 4,000 words (32,000 bytes).
(Document started on 25 Mar 2011.)
This is a WWW document maintained by
Steve Draper, installed at http://www.psy.gla.ac.uk/~steve/best/effect.html.
You may copy it.
How to refer to it.
Web site logical path:
[www.psy.gla.ac.uk]
[~steve]
[best]
[this page]
Effect size
By
Steve Draper,
Department of Psychology,
University of Glasgow.
Preface
This page is mainly about "effect size", which is a concept that tries to
remedy some of the deficiencies of just doing significance testing.
There is an emerging argument that effect size does not solve all those
deficiencies: see the last section
"Beyond effect sizes".
Main part of this page
This page is about effect size (ES): what it is in a slightly wider
perspective than just statistics. If you just want the statistical view and
tests, the wikipedia page seems good.
Also see this:
Mike Clark's
PDF local copy of his slides
on effect sizes.
Whereas statistical tests such as a t-test aim to tell you what degree of
certainty to attribute to the possibility that a difference is not an accident
but an effect, another important question
is "How important is that difference (if real)?". I shall use the term
"effect size" as a general title for this whole question;
group all statistical tests of effect size into one topic within the general
question; and the issue of which of the alternative stats tests
(e.g. "Cohen's d") is best as a subtopic.
Bloom84 gives a powerful argument about how to use
effect sizes in planning a programme of applied research.
The main point of measuring effect sizes is to compare the relative importance
of different effects, phenomena. An example from psychology illustrates this,
by comparing established gender effects -- and how some are really big, but
many others of small, even negligible, practical importance.
Comparing effect sizes: getting a sense of the range
A table of gender effects in psychology published by New Scientist is very
helpful in demonstrating how very different in magnitude effects can be.
These would be even better by using sections below to bring out
predictions, given a specific effect size e.g. the CLES which tells you what
are the chances, if you pick one random male and one random female, of them
differing on a given effect in the predicted direction.
I.e. It would be good to add a 3rd col. that shows the odds, given 1M and 1F
randomly taken, having a difference in the trait in the same direction as the
diff. in the means for that trait.
New Sci, Gender effects table
Explanation of the table below:
Diff. between males and females
(effect size in StdDev units).
Colour of the number shows which sex does better.
There are 6 more items in (the bottom of)
the original table.
| TRAIT |
Effect size |
Odds of one random pair showing the effect |
| Gender identity |
11.0 - 13.2 |
- |
| Sexual orientation |
6.0 - 7.0 |
- |
| Preference for boy's toys |
2.1 |
0.92 |
| Height |
2 |
0.92 |
| Preference for girl's toys |
1.8 |
0.9 |
| Physical aggression |
0.4 - 1.3 |
0.72 |
| Empathy |
0.3 - 1.3 |
0.71 |
| Fine motor skills |
0.5 - 0.6 |
0.65 |
| Mental rotation |
0.3 - 0.9 |
0.66 |
| Assertiveness |
0.2 - 0.8 |
0.64 |
Alternative stats measures of effect size
Use r (correlation coefficient) as the measure: according to
Open Science Collaboration (2015)
"Estimating the reproducibility of psychological science"
Science vol.349 Issue 6251 pp.910-911
doi:10.1126/science.aac4716
Cohen94 suggests using confidence intervals.
Rough ideas on what size effects are small / medium / large
|
Micro |
Small |
Medium |
Large |
Huge or Very big |
Gigantic |
Cases: →
Measures ↓
|
Time of day effects on school tests [9] |
Difference between the heights of 15 and 16 year old girls
in the USA.[1] |
M vs. F verbal fluency[2] |
Difference between the heights of 13 and 18 year old girls
in the USA.[3] |
Female vs. Male height[4]
Learning in
school class vs. 1:1 tutoring[5] |
Biological sex affects gender identity[6] |
| Cohen's d |
e.g. ≤ 0.03 |
0.2 - 0.3 |
≈ 0.5 |
0.8 - or larger |
2 |
12 |
[7]
r (correlation coeff.)
[11] |
- |
0.1 - 0.3 ≈ 0.1 |
0.3 - 0.5 ≈ 0.3 |
0.5 ≈ 0.5 |
- |
- |
R2:
% of variance explained |
- |
1% |
9% |
25% |
- |
- |
| R2:
(≈ ≈ Partial eta-squared) |
- |
0.02 |
0.13 |
0.26 |
- |
- |
| Generalized eta-squared
{η_G^2}
[8]
|
- |
0.02 |
0.13 |
0.26 |
- |
- |
Partial eta-squared
(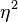 ) )
|
- |
0.01 |
0.06 |
0.14 |
- |
- |
| Odds ratio |
- |
- |
- |
- |
- |
- |
| Confidence interval |
- |
- |
- |
- |
- |
- |
Lit. refs for the table above
-
Mike Clark's
slides on effect sizes:
PDF on his web site
(PDF local copy).
- New Scientist table of gender-sex effects
table
Spinney, Laura (2011) "Boy brain, girl brain: How the sexes act differently"
New Scientist, no.2802, 8 March 2011
http://www.newscientist.com/article/mg20928021.400-boy-brain-girl-brain-how-the-sexes-act-differently.html
- See [1]
- See [2]
- Bloom84 mentions it.
- See [2]
- Cohen, J. (1988)
Statistical power analysis for the behavioral sciences (2nd ed.)
(Hillsdale, NJ: Erlbaum)
Also: Field,Andy (2013)
Discovering Statistics using IBM SPSS 4th edition p.267
- Cohen, J. (1988) cited above: p.286ff. for some of the effect sizes e.g.
for eta-squared.
- Bakeman, R. (2005)
"Recommended effect size statistics for repeated measures designs"
Behavior Research Methods vol.37 no.3 pp.379-384
doi:10.3758/BF03192707;
criticising Cohen (1988) (see [7]) pp.413-414.
- Sievertsen et al. 2016
- Cohen,J. (1992) "A power primer"
Psychological Bulletin Vol.112. No.1 pp.155-159
doi:10.1037/0033-2909.112.1.155
In this paper, Cohen expresses small, medium and large effect sizes, not as a
range of values, but in terms of a central value for each category.
Other notable cases include:
- Very big.
Particle physicists require a (Cohen's d) effect size of 5
(between "Very Big" and "Gigantic") before declaring the discovery
to have been established of a new particle (e.g. the Higgs boson)
(wikipedia entry).
- Very small.
This paper about the effect on school tests of the time of day when
the child takes it,
Sievertsen et al. 2016,
has a huge dataset, impeccable stats, and goes the extra mile by providing
information to help judge the data against relevant contextual standards. But
the effect sizes are still minute: a new category of "micro".
It reports a variety of (Cohen's d) effect sizes in the range 0.03 - 0.005.
Different meanings for "Important", and so for "effect size"
The basic idea is that sigDiffs at best only tell you how likely it is that
something is a true effect, but we should be asking how important a
finding is; and "effect size" is meant to be a measure of this.
But there are different senses of "important" for effects.
Some different senses of "how important" (A plan for future subsections)
- First: senses of the basic 'how important is this effect'?
- Contextual issues: what comparisons in each given context are relevant
in interpreting whether a given shift (in the mean) is important.
- Comparing to what other effects / causes? Even if the experiment
did not directly compare to some reference condition, this may be what
most readers would find meaningful e.g. comparing a drug to "treatment
as usual"; comparing an anti-depressant to regular exercise (now
surely the most relevant comparison).
- Comparing in what units? e.g. in education, giving an effect size
in statistical units may not be as meaningful as in an external
unit such as grades e.g. "the intervention increased learners' grades on
average by 0.5 (or by 2) grades".
- Comparing in what units? e.g. in education, giving an effect size
in statistical units may not be as natural as reporting in an
intrinsic unit e.g.
the intervention resulted in the absolute amount learned (normalised
gain) in the experimental group was 2 (or in fact 3) times that learned
in the control group (Crouch & Mazur 1993?).
- What proportion of the sample (or population) did the effect apply to?
- Somewhere have a section on really big and really small specifically
educational effects (including chick-sexing).
- Cost-effectiveness. In almost any practical context it isn't just an
issue of how much good you do, but also of how cheaply it can be done
— because with a given amount of resource, you can do more good to more
people by a cheap effect than by an expensive one.
- Unexpectedness w.r.t. theory
What proportion of the sample (or population) did the
effect apply to? [C]
#idiff
Guillaume Rousselet in
this blogpost raises this point.
If the variability in the data is just "noise" in the measurement process,
then the effect is actually true of all participants, but measurement
inaccuracies have blurred this; and "effect size" is just a metric of
measurement quality.
However if the variability is in the mechanism, and particularly in the common
but very important case of it being in the participants, then it is of great
interest e.g. a drug works on some people, but not others (e.g. because of
differing genetic heritage, or differing lifestyle protective factors, etc.).
This is common in looking at the effects of treatments or interventions; but
equally important for cases of "natural immunity" where for some people,
exposure doesn't lead to illness. This applies in many areas not just disease.
E.g. In Milgram's experiment, most did what the man in the white coat said
despite their qualms, but (just as importantly in Milgram's view)
15% were "immune" and did not.
Similarly priming and expectation effects may well work on some and not on
others: which is quite different from their working uniformly but weakly on all.
Or in positive psychology, gratitude exercises reliably raise well-being in
most, yet strongly religious or spiritual individuals seem "immune".
In these cases, it is of great interest to report what the proportion is
of the sample to which it applies. You may or may not agree with Rousselet's
labelling of this as a type of "effect size", but perhaps you should in any
case consider doing this routinely. Reporting the percentage is useful; a sign
test gives the probability of this being by chance.
Note that in this case, really the tacit hypothesis is that the distribution
is not normal, but bimodal: a population for which the effect "works", and
another for which it doesn't.
Basic approach: StdDev units
If you have a result with a strong p-value and good effect size, then what
does it predict specifically? This section is to explore the arithmetic of the
normal distribution to spell this out.
- Given a specific ES, show what % of the old data would be passed.
The table above is 2-tailed. But with a proven effect with an effect
size of 2 (for example) we probably want to know how much of the original data
is above 2 stdDevs (one-tailed).
To calculate this:
- Go to
this online calculator;
- (Leave the mean set to 0, the SDev to 1, and the radio
button "Above" selected;)
- Fill in "2" in the box beside "Above", and click "Recalculate".
It will show the "Area" as 0.0228, which means 2.28% of the data is more than 2
SDevs greater than the mean.
So if you applied an intervention with an effect size of +2, then without it
only 2.28% of a sample score that highly or better, but with it
50% will score that highly.
- If I took one Participant from the midpoint (mean = median) of the old
distribution, applied the intervention to her/him alone, then where would we
expect them to move to relative to the old distribution? ==
They were at percentile 50, they would move to which percentile?
[E.g. ES = 2, then percentile 50 --> 98; rank 50 --> 2nd]
[E.g. ES = 1, then percentile 50 --> 84; rank 50 --> 16]
- [weather extreme events]
Given a (small) shift in the mean, what does this do for frequency of datum-s
up at the extreme of a distribution? E.g. 100 year storms.
- Odds, in gender effects, of randomly picking 1 M, then 1 F and having the
difference on the measure be in the expected direction. Or not.
Equally for any effect, pick one value from control group and one from expt
group: what chance of these two data being in the expected order.
Then say:
How much in percentiles does a given ES mean?
Or for A vs. B: for a given ES, what are the odds of a random A and B that
they show the right direction for the overall effect?
CLES: chances of a random pair showing the effect
CLES = common language effect size.
It is the odds (or chance) of picking one random individual from each of the
control and expt. groups, and finding that the direction or size of the mean
difference of the groups applies to those cases.
See Coe: It's the Effect Size, Stupid.
How much of the variance is explained
Other sections / issues about effect size
Cases with small stats effect size, yet importance of other kinds
Sievertsen
Claims his effect is ethically important. This would be an example of another
kind of importance. However his particular claim is false: spending money on
levelling a minute injustice is to fail to spend it on more important
educational injustices such as parental wealth, parental support of education
in the home by their attitudes, etc.
Carrying plants out of hospital wards at night, back again during the day.
Unexpectedness w.r.t. theory [F]
Lecture theatre seating position (Perkins & Wieman, 2005).
Sig. (just about); low priority in practice; but important theoretically because
unexpected and we have no good explanation for this (small) effect.
I.e. if you want to do immediate practical good to learners, then low ES means
it isn't a good investment. However from the viewpoint of theoretical rather
than applied research, then the more unexpected an effect, the more valuable
it is regardless of effect size.
Put another way: a datum which is highly expected has little information
value, but one which is highly unexpected (if it can be trusted) has very high
information content.
Put still another way: for theory-directed research especially,
the importance of an effect does not only depend on the size of the difference
between an actual observation and a theory-predicted observation but also on
the confidence in the surprising measure and the confidence in the prediction.
This is also a way to begin to think about how to reason about the relative
value of different bits of qualitative research.
Cost effectiveness [E]
Aveyard and the 30 sec. GP consultation. Contains a CE analysis; and importance
depends strongly on this. Not a very large effect, but well worth the money for
the effect.
Similarly the Open University strengths intervention.
Aveyard et al. (2016)
"Screening and brief intervention for obesity in primary care:
a parallel, two-arm, randomised trial"
The Lancet doi:10.1016/S0140-6736(16)31893-1
Wright Brothers
In Engineering, there are cases where a single design was so obviously
superior to all previous ones that statistics are irrelevant, and in fact
silly. In such cases everyone following imitates most features of that design.
And they do not wait cautiously for evidence about its success: the first
demonstration is convincing, and those who wait are simply the ones who don't
become contributors to the field. The Wright Brothers aircraft, and
Stephenson's Rocket are 2 such examples.
"They made the first controlled, sustained flight of a powered,
heavier-than-air aircraft on December 17, 1903, four miles south of Kitty
Hawk, North Carolina, USA." "The brothers' fundamental breakthrough was their
invention of three-axis control, which enabled the pilot to steer the aircraft
effectively and to maintain its equilibrium. This method became
and remains standard on fixed-wing aircraft of all kinds."
By 1909? the modern aircraft had arrived.
By 1910 it had been used usefully by the military (both reconnaissance, and
dropping bombs).
Robert Stephenson's "Rocket" steam railway locomotive (1829):
- Single pair of driving wheels.
- * Multiple fire tube boiler
- * Blast pipe: using exhaust steam to force a draft through the fire and boiler.
- Less vertical, more nearly horizontal cylinders: better ride of the loco on
the track.
- * Pistons directly connected to driving wheels (no gearing used).
- Firebox separate from boiler. I.e. water jacket round firebox was primary
heating place; firetubes in boiler did additional heating.
Hake survey
Hake's survey is convincing without thinking about effect size statistically.
Why?
The overwhelming preponderance? ....
Meta-analysis
Here is an example of trying to influence practice (and policy) using effect
sizes reported from meta-analyses.
https://educationendowmentfoundation.org.uk/evidence-summaries/teaching-learning-toolkit/
Misc.
Odds ratio
I need to understand this; to understand why wikiP says it is a measure of ES,
and integrate it in this page.
Effect size for non-parametric stats
Notes to be addressed
Coe: It's the Effect Size, Stupid
http://daniellakens.blogspot.co.uk/2015/01/always-use-welchs-t-test-instead-of.html
References
Aveyard et al. (2016)
"Screening and brief intervention for obesity in primary care:
a parallel, two-arm, randomised trial"
The Lancet doi:10.1016/S0140-6736(16)31893-1
Bakeman, R. (2005)
"Recommended effect size statistics for repeated measures designs"
Behavior Research Methods vol.37 no.3 pp.379-384
doi:10.3758/BF03192707;
[criticising Cohen (1988) pp.413-414. ]
Bloom, B.S. (1984)
"The 2 Sigma Problem: The Search for Methods of Group Instruction as Effective
as One-to-One Tutoring"
Educational Researcher vol.13 no.6 (Jun. - Jul., 1984) pp.4-16
www.jstor.org/stable/1175554
Cohen, J. (1988)
Statistical power analysis for the behavioral sciences (2nd ed.)
(Hillsdale, NJ: Erlbaum)
Cohen,J. (1992) "A power primer"
Psychological Bulletin Vol.112. No.1 pp.155-159
doi:10.1037/0033-2909.112.1.155
Crouch, C.H. and Mazur, E. (2001), "Peer Instruction: Ten years
of experience and results", American Journal of Physics,
vol.69, no.9 pp.970-977
doi: 10.1119/1.1374249
Also available at
https://www.usna.edu/Users/physics/rwilson/_files/documents/peer.pdf
http://mazur-www.harvard.edu:16080/publications/Pub_263.pdf
Field,Andy (2013)
Discovering Statistics using IBM SPSS 4th edition p.267
Hake,R.R. (1998) "Interactive-engagement versus traditional methods: A
six-thousand-student survey of mechanics test data for introductory physics
courses" Am.J.Physics vol.66 no.1 pp.64-74
PDF copy
Hattie, John A.C. (2009) Visible learning: a synthesis of over
800 meta-analyses relating to achievement (London: Routledge)
GU lib record=b2650342
Myburgh,S.J., (2016)
Critique of Hattie
Perkins,K.K. and Wieman,C.E. (2005)
"The Surprising Impact of Seat Location on Student Performance"
The Physics Teacher vol.43 January pp.30-33
doi:10.1119/1.1845987
Sievertsen et al. (2016)
"Cognitive fatigue influences students' performance on standardized tests"
PANAS (Proc. National Academy of Sciences of the USA)
doi:10.1073/pnas.1516947113
Beyond effect sizes
There is a new argument emerging that effect sizes do not solve the most basic
problems with significance testing, which (so it goes) are:
- Picking a p-value of 0.05 is arbitrary and just a convention that doesn't
suit all situations. The same is just as true of effect size categories of
"medium" etc., as Cohen admitted.
- It doesn't solve the issue that experiments should be able to tell us when
there is NO effect as well as when there is one i.e. they should be able to
quantify the certainty derived from negative as well as positive evidence.
It was Fisher, working on stats for plant genetics,
who introduced the use of p-values and conventions. At the same time
Jeffreys, working on stats for
geological samples, introduced a different approach as expounded in the refs
below.
Zoltán Dienes (2008)
Understanding Psychology as a Science:
An Introduction to Scientific and Statistical Inference
(Palgrave Macmillan: London)
GU lib record=b2669949
Web site logical path:
[www.psy.gla.ac.uk]
[~steve]
[best]
[this page]
[Top of this page]
 )
)
 )
)